Answer:
Step-by-step explanation:
Given the functions:
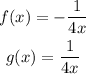
In order to know if the functions are inverses of each other, we must show that f(g(x)) is equal to g(f(x)).
Get the composite function f(g(x))
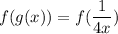
To get f(g(x)), we will replace the variable "x" in f(x) with 1/4x as shown:

Next is to get the composite function g(f(x))
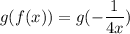
To get g(f(x)), we will replace the variable "x" in g(x) with -1/4x as shown:
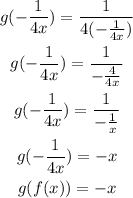
From the solution above, since f(g(x)) = g(f(x)) = -x, hence the functions f(x) and g(x) are