Arithmetic Sequence is a sequence of numbers such that the difference between each number is constant. The formula for the arithmetic sequence is given by;

where An is the last term
A₁ is the first term
n is the number of terms (or number in the sequence)
d is the common difference
In our problem we are given the first term (a₁) = 2, a common difference of 5 (d = 5), and the number of terms which is 29 (n = 29).
Now in order to find the 29th term of the sequence (a₂₉), we just need to follow the formula;
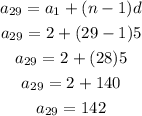
Therefore the 29th term of the arithmetic sequence is 142.