If two angles are complementary, their sum equals 90º
So if A and B are complementary we can say that:
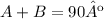
For
A=9x-3
B=10x-2
This equation is equal to
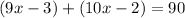
From this on you can solve for x:
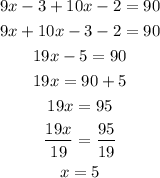
Now that the value of x is known, replace it in the expressions for A and B to determine the measure of the angles:
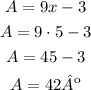
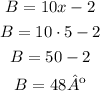
∠A=42º and ∠B=48º