Given the expression:
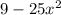
9 is the exact square of 3
25 is the exact square of 5
So you can rewrite this expression as:
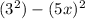
Now considering the formula for the difference of squares:
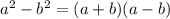
If we consider a=3 and b=5x, we can say that
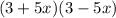
So we have that the steps to factor the given expression are:
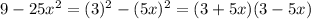
*-*-*-*-*-
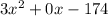
In this case, none of the terms is a perfect square, so you have to use another method.
I'll ignore the 0x term, since its irrelevant, the expression is then:

Both 3 and 147 are divisible by 3, so the first step will be to divide the expression by three to simplify it:
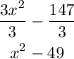
Now the terms of the equation are expressed as exact squares.
x²= x*x
and
49=7²=7*7
We reached the lowest simplification, now we can determine the diference of squares using a=x and b=7
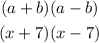
Finally multiply the factoring by 3 → at the begining we divided it by 3 to simplify the expression but if you dont multiply the final factoring by 3 again the result won't be equivalent to the original equation.
So the factoring of 3x²+0x-147 is 3(x+7)(x-7)