Question

Middle School plans to sell ice cream at a charity event. They expect to sell about 110 scoops of ice cream. The ice cream comes in cylindrical cartons. A carton of ice cream has a radius of 11cm and height of 30 cm. A scoop of ice cream has a radius of 3cm.a. How many cartons of ice cream should Ester order to make 100 scoops?9) Ester finds 50 souvenir glass cups leftover from the last charity event. The cup is a cone-shape and has a height of 16cm. and a radius of 3cm. The cup is filled and then topped with a half a scoop of ice cream.a. How much ice cream do they need to make 50 cups?b. If the 50 cups are in addition to the 100 scoops from #8a, how many more cartons of ice cream must Ester order?

Answer 1

This problem describes a situation where an event wishes to sell 110 scoops of ice cream in cylindrical cartons. Each carton has 11 cm in radius and a height of 30 cm. Each scoop of ice cream has a radius of 3 cm. We need to determine how many cartons of ice cream we should order to make 100 scoops.

We need to determine the volume of each scoop, since they're spheres with radius of 3 cm, the volume is given by:

`V_(Scoop)=(4)/(3)\pi(3)^3=113.1\text{ cubic centimeters}`

Now we need to determine the volume of the cartoons:

`V_(cartons)=\pi(11)^230=11403.98\text{ cubic centimeters}`

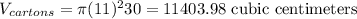
Now we need to multiply the volume of each scoop by 100:

`V_(icecream)=100\cdot113.1=11310\text{ cubic centimeters}`

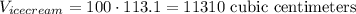
Since the volume for 100 scoops is less than the total volume for one carton, we can buy a single carton for 100 scoops.

For the second part, we need to calculate how much ice cream she will need to fill 50 cups that have a cone shape, she also intends to put a half scoop on top. We can draw the following situation to better represent the problem:

We need to calculate the volume of each cup, which is done by calculating the volume of the cone and the hemisphere that is on top of it:

`\begin{gathered} V_(cone)=\pi(3)^2(16)/(3)=150.8\text{ cubic centimeter}\\ \\ V_(hemisphere)=(2)/(3)\pi(3)^2=56.5\text{ cubic centimeter}\\ \\ V_(portion)=150.8+56.5=207.3\text{ cubic centimeter} \end{gathered}`

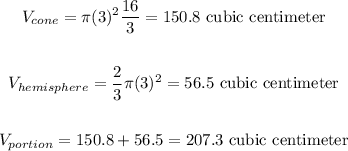
Now we need to multiply the volume for each portion by 50, to determine how much she will need for the 50 cups.

`V_(total)=50\cdot207.3=10365\text{ cubic centimeter}`

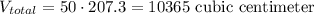
Now we need to add the volume for the 50 cups to the 100 scoops from before.

`V_(icecream)=10365+11310=21675\text{ cubic centimeters}`

Now we need to divide the volume of icecream we need by the volume of one carton:

`n_(cartons)=(21675)/(11403.98)=1.9`

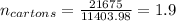
We need 2 cartons.