Question

TRIGONOMETRY what is the angle of the birds resultant vector?

Answer 1

Step-by-step explanation

We can represent the situation in the following picture:

By applying the trig. ratio we can get the angle of the resultant vector as shown as follows:

Assuming that the angle is called α,

`\tan \alpha=\frac{Opposite\text{ cathetus}}{\text{Adjacent cathetus}}=(12)/(45)=(4)/(15)`

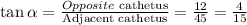
Applying tan^-1 to both sides:

`\alpha=\tan ^(-1)((4)/(15))`

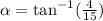
Computing the argument:

`\alpha=14.93\approx14.9^o`

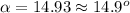
In conclusion, the angle is 14.9 degrees