Question

5. Write the equation of the line perpendicular2to y=x+3 that passes through the point5(-4,5).

Answer 1

First, we know that the slope of a perpendicular line given the equation of the line it is perpendicular can be found using the following equation:

`m_p=-(1)/(m)`

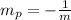
in this case, we have the line y = x + 3. Then, we have that its slope is m = 1, then, the perpendicular slope is:

`\begin{gathered} m=1 \\ \Rightarrow m_p=-(1)/(1)=-1 \\ m_p=-1 \end{gathered}`

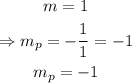
now that we have the slope of the perpendicular line, we can use the point (-4,5) and the slope-point formula to get:

`\begin{gathered} m_p=-1 \\ (x_0,y_0)=(-4,5) \\ y-y_0=m(x-x_0) \\ \Rightarrow y-5=-1(x-(-4))=-(x+4)=-x-4 \\ \Rightarrow y=-x-4+5=-x+1 \\ y=-x+1 \end{gathered}`

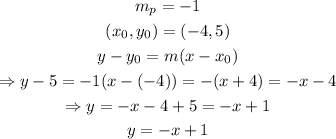
therefore, the equation of the line perpendicular to y = x+3 and passes through the point (-4,5) is y = -x + 1