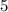Solution:
Given the triangle below where K is in the incenter:
Thus, we have
step 1: In the triangle DGK, find DK.
Thus, by Pythagoras theorem, we have

step 2: In the triangle KDI, find DK.
Similarly, we have
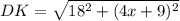
Step 3: Equate the equations in steps 1 and 2.
This gives

The value of x is