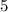Question

Determine the value of x for the triangle below if K is the incenter.E9.x-16X =لاGDHK184x + 9

Answer 1

Given the triangle below where K is in the incenter:

Thus, we have

step 1: In the triangle DGK, find DK.

Thus, by Pythagoras theorem, we have

`DK=√(18^2+(9x-16)^2)`

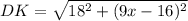
step 2: In the triangle KDI, find DK.

Similarly, we have

`DK=√(18^2+(4x+9)^2)`

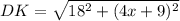
Step 3: Equate the equations in steps 1 and 2.

This gives

`\begin{gathered} √(18^2+(9x-16)^2)=√(18^2+(4x+9)^2) \\ take\text{ the square of both sides,} \\ \Rightarrow18^2+(9x-16)^2=18^2+(4x+9)^2 \\ thus,\text{ we have} \\ 9x-16=4x+9 \\ add\text{ -4x to both sides,} \\ 9x-4x-16=-4x+4x+9 \\ 5x-16=9 \\ add\text{ 16 to both sides,} \\ 5x-16+16=9+16 \\ \Rightarrow5x=25 \\ divide\text{ both sides by the coefficient of x, which is 5} \\ (5x)/(5)=(25)/(5) \\ \Rightarrow x=5 \end{gathered}`

The value of x is

`5`