Question

determine whether rolle’s theorem applies to the function. if it applies find all possible values of c

Answer 1

• Yes

,

• c=0

Step-by-step explanation:

Given the function, G(x):

`G(x)=(4)/(x^2+16)`

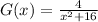
Rolle's Theorem:

According to this theorem if the given function is:

• continuous in [a,b]

,

• differentiable in (a,b)

,

• f(a) = f(b)

then, there exist c in (a,b) such that f'(c)=0.

Continuity of function:

Since the given function is continuous function, it is continuous everywhere. Therefore, G(x) is continuous in [-2,2]

Differentiability

The rational function is differentiable using the quotient rule. Therefore, G(x) is differentiable in (-2,2).

Next, evaluate G(-2) and G(2):

`\begin{gathered} G(-2)=(4)/((-2)^2+16)=(4)/(4+16)=(4)/(20)=(1)/(5) \\ G(2)=(4)/((2)^2+16)=(4)/(4+16)=(4)/(20)=(1)/(5) \\ G(-2)=G(2) \end{gathered}`

Thus, Rolle's theorem applies on G(x).

Next, we find the possible values of c.

By Rolle's theorem, there exist c in (a,b) such that f'(c) = 0.

`\begin{gathered} G(x)=(4)/(x^2+16) \\ G(x)=4(x^2+16)^(-1) \\ \text{Let u=}x^2+16\implies G(u)=4u^(-1) \\ (dG)/(dx)=(dG)/(du)*(du)/(dx)=-4u^(-2)*2x=-8x(x^2+16)^(-2) \\ G^(\prime)(x)=-(8x)/((x+16)^2) \end{gathered}`

Thus:

`\begin{gathered} G^(\prime)(c)=-(8c)/((c+16)^2)=0 \\ \implies-8c=0 \\ \implies c=0 \end{gathered}`

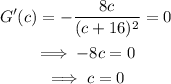
Since c should be in the interval [-2,2], the value of c that satisfies the theorem is 0.