Given information:
The velocity of the river is 2.8 m/s. The jet ski is at angle of 35° upstream. The velocity of the Jet ski relative to the ground is 9.5 m/s at an angle of 20° upstream.
The relative horizontal velocity of the Jet ski relative to the ground is,
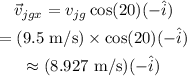
The relative vertical velocity of the Jet ski relative to the ground is,
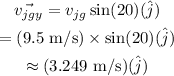
The relative velocity of the jet ski relative to the ground is,
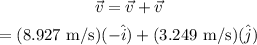
The relative velocity of the river relative to the ground is,

The relative velocity of the Jet ski relative to the river water is,

The magnitude of the relative velocity of the Jet ski relative to the river water is,
![\begin{gathered} v_(jr)=\sqrt[]{(8.927\text{ m/s})^2+(6.049\text{ m/s})^2} \\ \approx10.8\text{ m/s} \end{gathered}](https://img.qammunity.org/2023/formulas/physics/college/tc65cig43iwafhg3kcsphxb2m2r91zri3z.png)
Therefore, the speed of the Jet ski relative to the water is 10.8 m/s.