Question

The mean percent of childhood asthma prevalence in 43 cities is 2.35%. A random sample of 30 of these cities is selected. What is the probability that the meanchildhood asthma prevalence for the sample is greater than 2.7%? Interpret this probability. Assume that o = 1.27%The probability is a(Round to four decimal places as needed.)43

Answer 1

First, find the z-score.

`Z=\frac{x-\mu}{\frac{\sigma}{\sqrt[]{n}}}`

Using the given information, we have

`Z=\frac{2.7-2.35}{\frac{1.27}{\sqrt[]{43}}}\approx1.32`

Then, use a z-table to find the p-value of 0.9147.

At last, subtract this p-value from 1 to find the probability that the sample is greater than 2.7%.

`1-0.9147=0.0853`

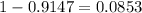
Therefore, the probability is 0.0853.