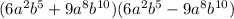Question

Factor the expression 36a^4 b^10 - 8 1a^16 b^20 using the two different techniques listed for Parts 1(a) and 1 (b).(a) Factor the given expression using the GCF monomial.(b) Factor the given expression using the difference of squares.

Answer 1

In this problem, we need to factor a given binomial using two different techniques.

We are given

`36a^4b^(10)-81a^(16)b^(20)`

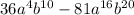
GCF Technique

The first technique we'll use is finding the greatest common factor of both terms. We'll look at each constant and variable separately.

`\begin{gathered} GCF(36,81)=9 \\ \\ GCF(a^4,a^(16))=a^4 \\ \\ GCF(b^(10),b^(20))=b^(10) \end{gathered}`

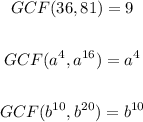
Therefore, the overall GCF of the binomial is:

`9a^4b^(10)`

We can factor it from each term to get:

`9a^4b^(10)(4-9a^(12)b^(10))`

Difference of Squares

In the second technique, we are going to apply the difference of squares.

`a^2-b^2=(a+b)(a-b)`

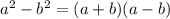
To get it into that form, we need to rewrite each term of the binomial as a square:

`\begin{gathered} 36a^4b^(10)\rightarrow(6a^2b^5)^2 \\ \\ 81a^(16)b^(20)\rightarrow(9a^8b^(10))^2 \end{gathered}`

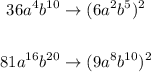
Now we can write it as

`(6a^2b^5)^2-(9a^8b^(10))^2`

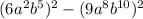
Using our rule, we get

`(6a^2b^5+9a^8b^(10))(6a^2b^5-9a^8b^(10))`