Question

If f(x) = 3x ^ 2 - 7x + 5 , find f^ prime (-4) .

Answer 1

Given:

`f(x)=3x^2-7x+5`

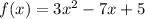
To determine f'(-4), we first find the derivative of the given equation as shown below:

`\begin{gathered} f(x)=3x^(2)-7x+5 \\ f^(\prime)(x)=6x-7 \end{gathered}`

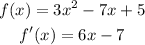
Next,we plug in x=-4 into f'(x)=6x-7:

`\begin{gathered} f^(\prime)\left(x\right)=6x-7 \\ f^(\prime)(-4)=6(-4)-7 \\ Calculate \\ f^(\prime)(-4)=-31 \end{gathered}`

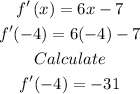
Hence, the value of f'(-4) is equal to -31.

Then, we also note that we can find the slope by plugging in x=-4 into f'(x)=6x-7.

Hence, the value of m is: -31

`m=-31`

Then,we use the point slope form:

`y-y_1=m(x-x_(1_))`

where:

m=slope=-31

(x1,y1)=point=(-4,81)

We plug in what we know:

`\begin{gathered} y-y_1=m(x-x_(1_)) \\ y-81=-31(x-(-4)) \\ Simplify\text{ and rearrange} \\ y-81=-31(x+4) \\ y-81=-31x-124 \\ y=-31x-124+81 \\ y=-31x-43 \end{gathered}`

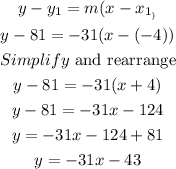
Since the equation of the tangent line can be written in y=mx+b, the value of b is equal to -43.

Therefore, b is: -43