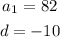
Step-by-step explanation
In an Arithmetic Sequence the difference between one term and the next is a constant. In other words, we just add the same value each time , it is given by the expression
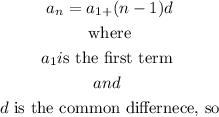
Step 1
Set the equations:
a)
Let
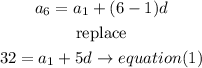
b)
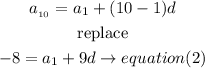
Step 2
Now, solve the equations
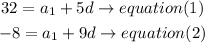
a) isolate a1 in equation (1) and then replace in equation (2)
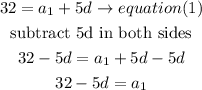
replace i equation (2)

b) now , fo find a1, replace d in equation(1)
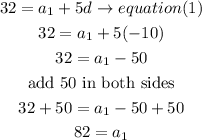
therefore, the answer is
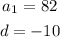
I hope this helps you