Answer: 45 is a counterexample of the expression
Given:

Let us first write sec and tan in terms of cos and sin functions:
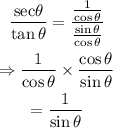
We now have:
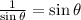
As we can see, the two expressions are not equal, therefore:
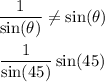
Since the two expressions are not equal, 45 is a counterexample of the expression.