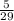Solution
- Probability of an event A is defined by:
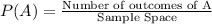
- Randomly choosing multiples of 5 between 21 and 49, we have:
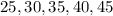
-There are 5 numbers in total. This means that the Number of Outcomes is 5.
- Between 21 and 49, there are 29 numbers. This represents the Sample Space.
- Thus, we can proceed to find the probability of choosing a multiple of 5 between 21 and 49 as follows:

Final Answer
The answer is