The Solution:
Given:
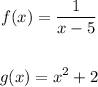
Required:
Part II:
Find the values of:
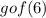
Step 1:
Find g(f(x) by substituting f(x) in the place x in g(x).
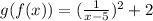
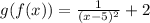
Step 2:
Find the value of g(f(6)).
Substitute x = 6 in g(f(x)).
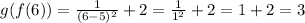
Alternatively:
Substitute x = 6 in f(x).
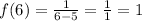
Substitute f(6) = 1 in g(x) to get g(f(6)).
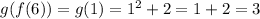
Answer:
g(f(6)) = 3