Question

David has a bag that contains strawberry chews, apple chews, and watermelon chews.He performs an experiment. David randomly removes a chew from the bag, recordsthe result, and returns the chew to the bag. David performs the experiment 63 times.The results are shown below:A strawberry chew was selected 35 times.A apple chew was selected 8 times.A watermelon chew was selected 20 times.If the experiment is repeated 1700 more times, about how many times would youexpect David to remove a strawberry chew from the bag? Round your answer to thenearest whole number.

Answer 1

The expected number of times that a strawberry chew was removed is 944

Step-by-step explanation:

We need to find the probability of taking a strawberry chew (SC). The formula for the probability of an event A occurring is:

`P(A)=\frac{favorable\text{ }outcomes}{total\text{ }outcomes}`

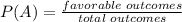
The total outcomes are the number of times David removed a chew: 63. The favorable outcomes are the number of times a SC was removed: 35.

Then:

`P(SC)=(35)/(63)=(5)/(9)`

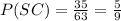
Now, if we multiply the probability times the number of times we repeat the experiment of removing a chew from the bag, we get the expected number:_

`1700\cdot(5)/(9)\approx944.44`

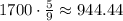
To the nearest whole, 944