Question

Question 5 of 9Which of the expressions are equivalent to the one below? Check all thatapply.6.(2+8)I A. (8 + 2). 6OB. 6. (8 + 2)O C. 6. 2) + 8O d. 6.2 + 6.8SUBMIT

Answer 1

We have the expression:

`6\cdot(2+8)`

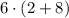
We can solve the parenthesis and then multiply or we can apply the distibutive property before the addition.

1) Solving the parenthesis first:

`6\cdot(2+8)=6\cdot10=60`

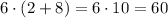
2) Applying the distributive property:

`6\cdot(2+8)=6\cdot2+6\cdot8=12+48=60`

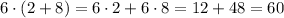
If we look at each of the expressions, we can find if they are equivalent of not.

A) Equivalent. In this case, we are applying the commutative property of the multiplication (you can multiply in any order).

`6\cdot(2+8)=(2+8)\cdot6`

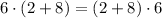
B) Equivalent. In this case, the commutative property of the addition is applied, as we can sum in any order.

`6\cdot(2+8)=6\cdot(8+2)`

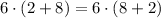
C) Not equivalent. Is the distributive property but applied wrong: the 6 has to also multiply the 8.

`6\cdot(2+8)\\eq(6\cdot2)+8`

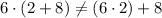
D) Equivalent. This is the application of the distributive property.