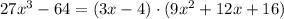Solve this problem using the difference of cubes formula, since both terms are perfect cubes.
According to the difference of cubes formula, given a³ - b³ = (a - b)(a² + ab+ b²).
So, follow the steps to solve this problem.
Step 01: Find "a".
Comparing with the equation above:
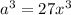
Take the cubic root from both sides:
![\begin{gathered} \sqrt[3]{a^3}=\sqrt[3]{27x^3} \\ a^{(3)/(3)=}\sqrt[3]{27}\cdot\sqrt[3]{x^3} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/ys9axuxrfocwyezezb8tce65zohqucroxr.png)
Factoring 27 = 3 * 3 *3 = 3³. Then,
![\begin{gathered} a=\sqrt[3]{3^3}\cdot\sqrt[3]{x^3} \\ a=3x \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/9pxe4svh3lkf0o30ku9i0e3931i7jbzpyo.png)
Step 01: Find "b".
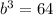
Taking the cubic root from both sides and factoring 64:
64 = 4*4*4. Then,
![\begin{gathered} \sqrt[3]{b^3}=\sqrt[3]{4^3} \\ b=4 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/vpfjboj1g1uacweubygozl6cfmp3v70kyh.png)
Step 03: Substitute "a" and "b" in the formula.
a³ - b³ = (a - b)(a² + ab+ b²).
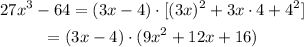
Answer: