Question

The formula A0.0466129emodels the population of a particular city, in thousands, t years after 1996.When will the population of the city reach 164 thousand?1990200120031991

Answer 1

Since the equation of population is

`A=129e^(0.046t)`

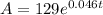
Where A is the population of thousands after the year 1996

We need to find the year that has a population of 164 thousand

Then substitute A by 164

`164=129e^(0.046t)`

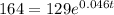
Divide both sides by 129

`\begin{gathered} (164)/(129)=(129e^(0.046t))/(129) \\ (16)/(129)=e^(0.046t) \end{gathered}`

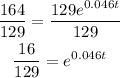
Insert ln on both sides

`ln((164)/(129))=ln(e^(0.046t))`

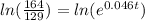
Use the rule of ln to simplify

`ln(e^m)=m`
`ln((164)/(129))=0.046t`

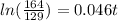
Divide both sides by 0.046 to find the value of t

`\begin{gathered} (ln((164)/(129)))/(0.046)=(0.046t)/(0.046) \\ 5.218565727=t \\ 5\approx t \end{gathered}`

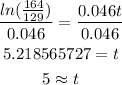
Then the population would be 164 thousand after about 5 years after 1996

Then to find the year add 5 to 1996

`1996+5=2001`

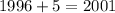
The population will be 164 thousand on 2001

The answer is 2001