Question

How do I find parts A, B and C. ( just little explanation needed but I just need the answer)

Answer 1

Part A

In parallel lines, because of the symmetry, some angles are equal.

In the following image we see in the same color the angles that are equal or congruent:

The yellow angles are equal, and the red angles are equal.

In this case, we are asked for the relationship between angles 1 and 8.

Angles 1 and 8 are alternate exterior angles.

Part B

Since alternate exterior angles are equal, we have for the values given in part B that:

`\begin{gathered} m\angle1=m\angle8 \\ (3x+50)=(5x-20) \end{gathered}`

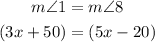
Part C

We need to find m∠2.

For that, first, we need to find the value of x by solving the equation from part B:

`\begin{gathered} (3x+50)=(5x-20) \\ 3x+50=5x-20 \\ 50+20=5x-3x \\ 70=2x \\ (70)/(2)=x \\ 35=x \end{gathered}`

Since x is equal to 35, angle 1 is equal to:

`\begin{gathered} m\angle1=3x+50 \\ m\angle1=3(35)+50 \\ m\angle1=155 \end{gathered}`

And in the image, we can see that angles 1 and 2 are supplementary angles: the sum of them is 180°:

`\begin{gathered} m\angle1+m\angle2=180 \\ \text{substituting m}\angle1=155 \\ 155+m\angle2=180 \\ \text{Subtracting 155 to both sides:} \\ m\angle2=180-155 \\ m\angle2=25 \end{gathered}`

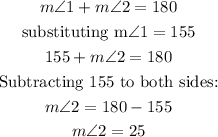
m∠2=25