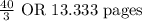Question

You might need: Henry can write 5 pages of his novel in 3 hours. At this rate, how many pages can Henry write in 8 hours?

Answer 1

We will investigate how to your direct proportions to evaluate the number of pages Henry can write given a set of time frame.

There is a relationship established between the number of pages that Henry writes in a certain amount off time. We will go ahead and define the variables:

`\begin{gathered} x\text{ = Amount of time ( hours )} \\ y\text{ = Number of pages written} \end{gathered}`

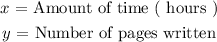
We see that there is a direct relationship between the two variables ( x and y ). We can express a direct relation with the following equation:

`y\text{ = k}\cdot x`

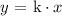
Where,

`k\text{ = constant of proportionality}`

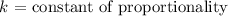
To determine the constant of proportionality ( k ) we need a set of data. I.e the number of pages written in an amount of time. We are given that Henry can write 5 pages of his novel in 3 hours. So:

`x\text{ = 3 , y = 5}`

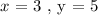
We will use the direct proportion relation expressed above and evaluate the constant of proportionality ( k ) as follows:

`\begin{gathered} 5\text{ = k}\cdot3 \\ \\ k\text{ = }(5)/(3) \end{gathered}`

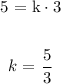
Therefore, the direct relationship between the two variables becomes:

`y\text{ = }(5)/(3)\cdot x`

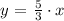
Now we can use the above relation to determine either off the two variables given the other one. We are asked to find the number of pages that Henry can write if he takes 8 hours. Hence,

`x\text{ = 8 , y = ?}`

Using the defined relationship we can calculate as follows:

`\begin{gathered} y\text{ = }(5)/(3)\cdot\text{ ( 8 )} \\ \\ y\text{ = }(40)/(3)\text{ = 13.333 pages} \end{gathered}`

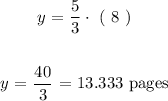
Therefore, the answer is:

`(40)/(3)\text{ OR 13.333 pages}`