Question

The value of Kc for the reaction below is 0.460 at 50.00°C and 0.650 at 100.00°CA --------> B <--------Calculate ΔH° for the reaction._______ kJ

Answer 1

Answer: the value of ΔH for the reaction given is 6.94 kJ/mol

Step-by-step explanation:

The question requires us to calculate the enthalpy change (ΔH) for the generic chemical equation given, provided the equilibrium constant (Kc) for this reaction at two different temperatures.

The following information was provided by the question:

T(1) = 50.00 °C

Kc(1) = 0.460

T(2) = 100.00 °C

Kc(2) = 0.650

We can apply the following equation to determine the enthalpy change of a reaction knowing the equilibrium constant at two different temperature:

`ln(K_2)/(K_1)=(\Delta H)/(R)((1)/(T_1)-(1)/(T_2))`

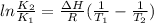
We can use the following value for R (the constant of gases):

R = 8.3145 J/mol.K

In order to make the calculation easier, we can "break down" the equation and calculate the parts for which the question provided the values, and then replace them back to the equation:

First, let's calculate part a:

`a=ln(K_2)/(K_1)=ln(0.650)/(0.460)=ln(1.41)=0.346`

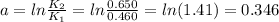
Next, let's calculate part b (note that the constant of gases, R, uses temperature in units of K, thus we'll need to convert the values of temperature given from Celsius degrees to Kelvin):

`\begin{gathered} T_1=50.00+273.15=323.15K \\ T_2=100.00+273.15=373.15K \end{gathered}`
`b=((1)/(T_1)-(1)/(T_2))=(1)/(323.15K)-(1)/(373.15K)=0.00041466K^(-1)`

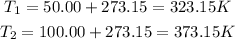
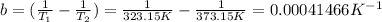
Now, we can return to the complete equation and replace the calculated values (a and b) along with the constant of gases:

`\begin{gathered} a=(\Delta H)/(R)* b\rightarrow\Delta H=(a* R)/(b) \\ \\ \Delta H=\frac{0.346*8.3145\text{ J/mol.K}}{0.0004166K^(-1)}=6.94*10^3\text{ J/mol = 6.94 kJ/mol} \end{gathered}`

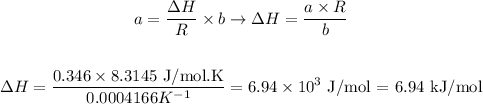
Therefore, the value of ΔH for the reaction given is 6.94 kJ/mol.