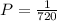Question

Short answer please Ten runners enter a race. The first-place runner will win a gold medal, the second-place runner will win a silver medal, and the third-place runner will win a bronze medal.a. How many different ways can the medals be awarded? b. What is the probability that out of the ten runners Susie, Jose, and Thomas are the first, second, and third place runners, in that particular order?

Answer 1

QUESTION A

The number of ways that we can pick the medals is given using the permutation:

`^(10)P_3`

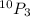
The permutation formula is given to be:

`^nP_r=(n !)/((n-r) !)`

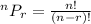
Therefore, the number of ways the winner can be chosen is calculated to be:

`^(10)P_3=(10!)/((10-3)!)=(10!)/(7!)=(10*9*8*7!)/(7!)=720`

Hence, there are 720 ways the medals can be awarded.

QUESTION B

The probability is calculated to be the ratio of the expected outcome to the total possible outcomes:

`P=\frac{Number\text{ }of\text{ }expected\text{ }outcomes}{Number\text{ }of\text{ }possible\text{ }outcomes}`

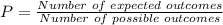
Picking Susie, Jose, and Thomas in that order is just one possible outcome.

Therefore, the probability of this outcome is:

`P=(1)/(720)`