1) Two lines are parallel when they have the same slope, for example, the lines:
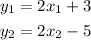
The coefficients of the x-terms of the lines are their slopes. In this example, both slopes are equal to 2, so the lines are parallel.
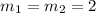
m₁ indicates the slope of the first line
m₂ indicates the slope of the second line
2) If two lines are perpendicular, then their slopes are reverse opposites, for example, given the lines:
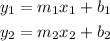
For both lines to be perpendicular the relationship between their slopes must be the following:
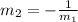
If a line has a slope m₁=3, then the slope of the perpendicular line will be:
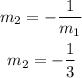
3) If the slopes are not equal nor reverse opposites, then the lines you are comparing are neither parallel nor perpendicular, for example, the lines:
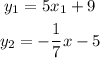
With this in mind, considering the given lines:
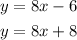
The slope of both lines is equal to 8, which means that the lines are parallel.