For this problem, we were informed that the variable "y" is directly proportional to the cube of x. We were also informed that y is equal to 9 when x is equal to 5, from this we need to determine the value of y when x is equal to 4.
Since the two variables are directly proportional, we can write them as shown below:
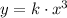
Where "k" is an unknown constant number that we need to determine. Since we have a point on this function (5, 9), we can determine "k" by replacing these coordinates on the expression.
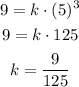
With the value of k, we can complete the expression:
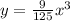
Now we can replace "x" with 4 to determine the value of y.
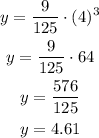
The value of y is approximately 4.61.