Question

An official playing field (including end zones) for the Indoor Football League has a length 38yd longer than its width. The perimeter of the rectangular field is 160yd. Find the length and width of the field.

Answer 1

Let's use the variable x to represent the width of the field.

If the length is 38 yd longer thatn the width, the length is equal to "x + 38".

Then, if the perimeter (which is the sum of all sides) is equal to 160 yd, we can write the following equation:

`\begin{gathered} \text{Perimeter}=2\cdot\text{length}+2\cdot\text{width} \\ 160=2\cdot(x+38)+2\cdot x \end{gathered}`

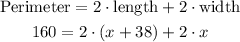
Solving this equation for x, we have:

`\begin{gathered} 80=x+38+x \\ 2x+38=80 \\ 2x=80-38 \\ 2x=42 \\ x=(42)/(2) \\ x=21\text{ yd} \\ \\ \text{length}=x+38=21+38=59\text{ yd} \end{gathered}`

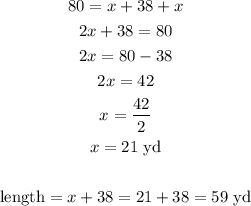
Therefore the length is equal to 59 yd and the width is equal to 21 yd.