Question

1. Suppose a single bacterium lands on one of your teeth and starts reproducing by a factor of 2 every hour. Ifnothing is done to stop the growth of the bacteria, write a function for the number of bacteria as a functionofthe number of days.

Answer 1

Answer: We can model the problem by using the following formula:

`F(t)=Ie^(rt)\rightarrow(1)`

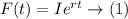
Where F is the final bacteria and I is the initial bacteria at the start, r is the doubling constant, and t is time:

`\begin{gathered} \begin{equation*} F(t)=Ie^(rt) \end{equation*} \\ \\ 4=2e^(r(1)) \\ \\ 2=e^r \\ \\ r=ln(2)=0.69314718055 \\ \\ r=0.693 \end{gathered}`

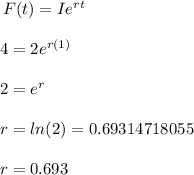
Therefore for the number of hours, the function is:

`F(t)=2e^(0.693t)\rightarrow(2)`

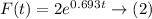
Similarly, for the number of days, the function is as follows:

`\begin{gathered} \begin{equation*} F(t)=Ie^(rt) \end{equation*} \\ \\ 33554432=2e^t \\ \\ r=ln((33554432)/(2))=16.636 \\ \\ r=16.636 \\ \\ \therefore\rightarrow \\ \\ F(t)=2e^(16.636t)\rightarrow(3) \end{gathered}`

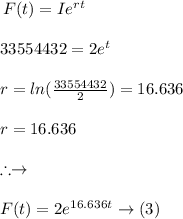
Equation (3) is the final function.