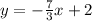Question

Write an equation in point-slope form and slope-intercept form of the equation of the line through the given points. Through (0, 2) and 3, -5).

Answer 1

The point-slope form of the equation of a straight line is given by the equation:

`\begin{gathered} y-y_1=m(x-x_1) \\ \text{where}\colon \\ (x_1,y_1)\text{ is one point on the line} \\ m\text{ is the slope of the line} \end{gathered}`

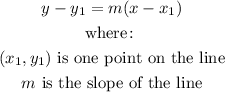
From the given points:

`\begin{gathered} (0,2)\text{ and (3,-5)} \\ x_1=0;y_1=2 \\ x_2=3;y_2=-5 \end{gathered}`

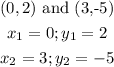
We have obtain the slope, m, of the line first. The slope is given by the equation:

`\begin{gathered} m=(y_2-y_1)/(x_2-x_1) \\ m=(-5-2)/(3-0) \\ m=(-7)/(3) \\ m=(-7)/(3) \end{gathered}`

Hence, the point-slope form is:

`\begin{gathered} y-2=-(7)/(3)(x-0)_{} \\ y-2=-(7)/(3)x \end{gathered}`

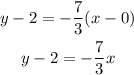
The slope intercept form of a straight line equation is given by the equation:

`\begin{gathered} y=mx+c \\ \text{where:} \\ m\colon\text{slope} \\ c\colon\text{intercept} \end{gathered}`

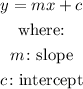
From the point-slope form, we can deduce the slope-intercept form of the equation.

Thus, we have:

`\begin{gathered} y-2=-(7)/(3)x \\ y=-(7)/(3)x+2 \end{gathered}`

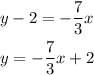
Hence, the slope-intercept form is:

`y=-(7)/(3)x+2`