Question

Find the angles and sides of the right triangle B = 70 degrees, b= 19ft. Please round to the nearest degree.

Answer 1

Data:

• B = 70°

,

• b = 19ft

,

• C = 90°

Procedure:

• Finding the angles

We know that C = 90° as the image shows the symbols. Also, we know that the sum of the interior angles of a triangle are 180°. Then, to get A we have to do the following:

`A+B+C=180`

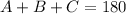
Isolating for A:

`A=180-B-C`

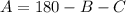
Replacing the values we know:

`A=180-70-90`
`A=20`

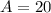
• Finding side ,a

Using trigonometric functions, we can get a.

`\tan (A)=(a)/(b)`

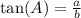
As we already know the value of A and b, we can isolate for a:

`a=b\cdot\tan (A)`

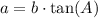
Replacing the values:

`a=19\cdot\tan (20)\approx6.92`

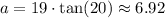
• Finding side ,c

Finally, using the Pythagorean Theorem, we can calculate c:

`c^2=a^2+b^2`

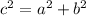
Isolating for c:

`c=\sqrt[]{a^2+b^2}`

Replacing the values:

`c=\sqrt[]{6.92^2+19^2}`
`c\approx20.22`

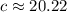
Answer:

• A = 20°

• a = 6.92 ft

,

• c = 20.22 ft