Question

Find the x-intercept(s) and the coordinates of the vertex for the parabola . I mathcal Z +xp+X-=K If there is more than one x-intercept, separate them with commas.

Answer 1

Answer :(a) Therefore , x - intercept: x = -3 and x = 7

(b) vertex point is at ( 2;33)

Explanation :

Given the parabola

`y\text{ = -x}^2+4x\text{ + 21 }`

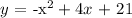
(i) Determine X - intercept( s)

by letting y = o

then :

`\begin{gathered} -x^2\text{ +4x +21 = 0 } \\ (x\text{ +3 \rparen \lparen-x +7 \rparen = 0} \\ \therefore\text{ \lparen x+3 \rparen = 0 ,,, then x = -3 } \\ \text{ \lparen-x+7\rparen = 0 ,,,,then x = 7 } \end{gathered}`

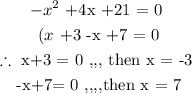
Therefore , x - intercept: x = -3 and x = 7

(ii) Determine the vertex : Method 1

Find the derivative of y , then solve for x and y - intercept :

`\begin{gathered} \frac{dy}{dx\text{ }}=\text{ \lparen-x}^2+4x\text{ +21\rparen }(d)/(dx) \\ \text{ = -2x +4 +0 } \\ \text{ = -2x +4 } \\ \text{ } \end{gathered}`

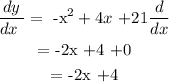
Then set , -2x+4 = 0

Therefore , x= -4 /-2 = 2

Method 2 :

Instead of using the derivative , we can apply the formula of x = -b/2a

• where a = -1 and b = +4

then ;

`x\text{ = }\frac{-b}{2a\text{ }}\text{ = -}\frac{4}{2(-1)\text{ }}\text{ = }\frac{-\text{4 }}{-2\text{ }}\text{ = 2 }`

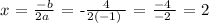
TAKE NOTE THAT OUR VALUE FOR X = 2

Substitute x = 2 into the original parabola, we get that

y = -(2)^2 + 4(2) + 21 = 4 +8 +21 =33

This means that our vertex point is at ( 2;33)