Question

For the second part, select the graph of the function.

Answer 1

ANSWER and EXPLANATION

We want to graph the given function:

`h(x)=√(x+8)`

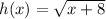
The function is a square root function. The parent function of all square root functions is:

`f(x)=√(x)`

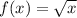
Now, we have to graph the parent function. To do this, we need three coordinate points that can be found by finding the value of the function at certain values of x.

Let us find the value of the function when x = 0, 4, 9:

`\begin{gathered} \Rightarrow x=0: \\ \\ f(x)=√(0)=0 \\ \\ \Rightarrow x=4: \\ \\ y=√(4)=2 \\ \\ \Rightarrow x=9: \\ \\ y=√(9)=3 \end{gathered}`

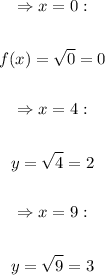
Now, we have three coordinate points: (0, 0), (4, 2), and (9, 3).

Let us plot the graph:

Now, to plot the given function h(x), we have to find the values of the function for certain values of x.

Let us find the value of the function for x = -8, -4, 1:

`\begin{gathered} \Rightarrow x=-8: \\ \\ y=√(-8+8)=√(0)=0 \\ \\ \Rightarrow x=-4: \\ \\ y=√(-4+8)=√(4)=2 \\ \\ \Rightarrow x=1: \\ \\ y=√(1+8)=√(9)=3 \end{gathered}`

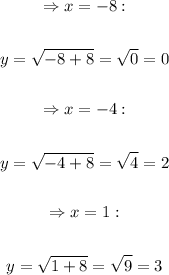
Now, we have three coordinate points for the graph of the function: (-8, 0), (-4, 2), and (1, 3).

Let us plot the graph now:

From the graph, the blue line represents the function h(x) while the red line represents the function f(x).

As we can see, the correct option for the graph of h(x) is option D.

The domain of a function is the set of all possible values of x for which the function is valid.

Therefore, the domain of the function is:

`[-8,\infty)`

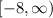
The range of a function is the set of all values of y i.e. output values of the function.

Therefore, the range of the function is:

`[0,\infty)`

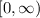
From the plotted graphs, we see that the values of the domain were 8 units less for each of the same values of the range. This implies that the domain of the graph has been shifted 8 units on the horizontal axis.

Therefore, the transformation that is needed to graph the function is that the graph if y = √x should be shifted horizontally to the left by 8 units.