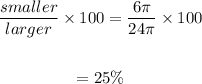ANSWER :
Surface area of larger cone : 24π units^2
Surface area of smaller cone : 6π units^2
The surface area of the smaller cone is 25% of that of the larger cone.
EXPLANATION :
From the given problem,
AB = 3 is the radius of the larger cone and the slanted height is BC = 5
DE = 1.5 is the radius of the smaller cone and the slanted height is EC = 2.5
Recall the surface area of the cone :
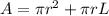
where r = radius and L = slanted height.
For the larger cone, r = 3 and L = 5
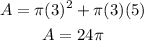
For the smaller cone, r = 1.5 and L = 2.5
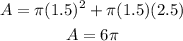
Comparing the surface areas :
The area of the smaller cone compared to the larger cone is :