Question

Hi! Could you help me with number 5? I believe the answer may be a reflection or something but i wanted to double check

Answer 1

Given the Pre-Image ABC and the Image DEF, you can identify that:

`C\mleft(-1,-2\mright)`

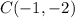
And the coordinates of the corresponding point after the transformation is:

`F\mleft(4,-2\mright)`

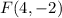
Notice that the y-coordinates do not change. The x-coordinates do change.

By definition, Reflections are transformations in which the figure is flipped over a line called "Line of reflection".

When a figure is reflected over any line, each point of the Image and each point of the Pre-Image has the same distance from the Line of Reflection.

In this case, you can identify this distance between points C and F:

Therefore, you can conclude that the line of reflection must be a vertical line that passes through:

`x=1.5`

In this form, point C and point F would be 2.5 units from the Line of Reflection.

See the picture below:

Notice that each corresponding point has the same distance from the green line (the line of reflection).

Hence, the answer is: A Reflection over the line:

`x=1.5`