Question

Solve using elimination. -6x - y = 13 9x – 4y = 19(_,_)

Answer 1

Solving by elimination method.

We have the following system of equations:

`\begin{gathered} -6x-y=13 \\ 9x-4y=19 \end{gathered}`

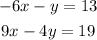
we can multiply the first equation by -4, then we have the equivalent system:

`\begin{gathered} 24x+4y=-52 \\ 9x-4y=19 \end{gathered}`

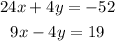
If we add both equations, we obtain

`\begin{gathered} 24x+9x=-52+19 \\ 33x=-33 \\ x=(-33)/(33) \\ x=-1 \end{gathered}`

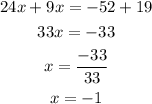
now, we can substitute this values into the first original equation, It yields

`\begin{gathered} -6(-1)-y=13 \\ \end{gathered}`

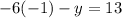
then, we have

`\begin{gathered} 6-y=13 \\ -y=13-6 \\ -y=7 \\ y=-7 \end{gathered}`

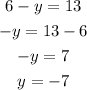
Therefore, the answer is x= -1 and y= -7, which correspond to the point (-1,-7).