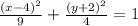To convert the given general form of the equation of the ellipse to standard form, here are the steps:
1. Group the terms with the same variable. Transfer the constant term on the other side of the equation.
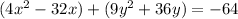
2. Extract a common factor on each group.
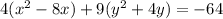
3. Apply completing the square method in each group in parenthesis to make it a perfect square trinomial. Divide the middle term by 2 and square it. The result will be the third term in each group.
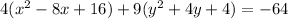
4. Multiply the constant term in each group to each respective factor and add the results to the other side of the equation.
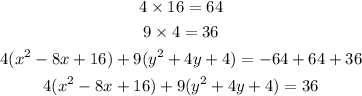
5. Rewrite each group of trinomial to binomial using its factors.

6. Lastly, divide both sides of the equation by the constant term 36.
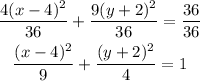
Hence, the equation of the ellipse in standard form is: