Question

The answers are not correct.Can you please solve it correctly for me

Answer 1

The interior angles of a regular pentagon measure 108°.

The segment that passes through the center of a pentagon and one of the vertices bisects this angle.

Taking this information into consideration we can draw a right triangle inside the pentagon with the next measures:

With the help of the tangent function, the length of x is:

`\begin{gathered} \tan (54\degree)=(6.2)/(x) \\ x=(6.2)/(\tan(54\degree)) \\ x\approx4.5\text{ }mm \end{gathered}`

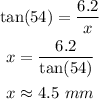
The length of the side of the pentagon is twice the length of x, that is,

`\begin{gathered} \text{ Length of the side of the pentagon = }2x \\ \text{ Length of the side of the pentagon }\approx\text{ }2\cdot4.5 \\ \text{ Length of the side of the pentagon }\approx9\text{ }mm \end{gathered}`

Formula for the area of a regular pentagon

`A=(1)/(4)\sqrt[]{5(5+2\sqrt[]{5})}\cdot a^2`

where a is the length of each side.

Substituting with a = 9 mm, we get: