It is important to note first the following:
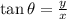
and
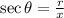
The first condition given in the question is tan θ > 0 hence, we can assume that both x and y are either positive or negative so that we can have a positive number.
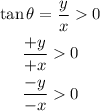
This means our θ falls either in Quadrant I or Quadrant III because the coordinate in Quadrant I are (+, +) while in Quadrant III is (-, -).
Now, the second condition given is that sec θ > 0, hence, we can assume that the value of "x" has to be positive so that sec θ will be greater than zero.
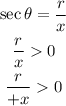
Between Quadrant I and Quadrant III, Quadrant I has a positive x value. Hence, θ is found in Quadrant I.