Question

Predict what will happen to the graph of the function f(x) = x1/3^ , if the function is changed to f(x) = (x-12)^1/3

Answer 1

We have the following function:

`f(x)=x^{(1)/(3)}`

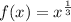
And we have to predict what would happen if the function changes to:

`f(x)=(x-12)^{(1)/(3)}`

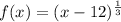
To predict what will happen in this case, we have that:

1. The first function is called the parent function.

2. The second function is a transformation of the parent function.

3. The given transformation is of the form:

`f(x-h)\rightarrow\text{ f\lparen x\rparen has been translated by h units to the right}`

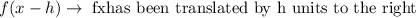
4. Then we have that, in this case, we have that the parent function has been translated 12 units to the right since we have:

`\begin{gathered} x^{(1)/(3)}\rightarrow(x-12)^{(1)/(3)}\text{ The parent function has been translated 12 units to the} \\ \text{ right.} \end{gathered}`

5. And we can check this if we graph the two functions as follows:

Therefore, in summary, we have that:

The graph will shift to the right 12 units (option C.)