consider the inequality
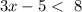
this is equivalent to:
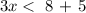
this is equivalent to
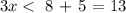
this is equivalent to say:
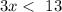
solve for x:
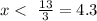
so, the correct answer for the second problem is (C) 4.5 , because 4.5 > 4.3 so 4.5 is not in the interval ( -infinity,4.3)
For problem 1, note that we have the following interval
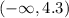
on the Real line that is: