Question

there are 20 runners in a marathon. the runner who in the top three places will recieve prizes how many different ways could the runners finish if there are three different prizes A= 8,000B= 6,840C= 57D= 201

Answer 1

You have 20 runners in the marathon, to determine how many different ways could you group the runners so that they end up in the first three places r=3 you have to calculate the permutation without repetition. We use permutation because the order matters, since the prize changes as the runner comes in first, second or third place.

It is without repetition because a runner cannot finish between the first three places twice at the same time.

The formula you have to use is

`(n!)/((n-r)!)`

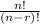
n is the total number of runners

r is the number we have to choose

`(20!)/((20-3)!)=6840`

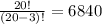
Correct option is B.