Question

I have to answer this question using trigonometry ratios to find the unknown angle measure or side length in the following problem.

Answer 1

Write out the given dimension with respect to the unknown angle

`\begin{gathered} \text{hypothenuse is the sides facing the right angle and the longest side of the triangle} \\ \text{The opposite is the side facing the unknown angle} \\ \text{adjacent is the side near the angle touching the hypothenuse} \end{gathered}`

From the right-angled triangle given,

`\begin{gathered} \text{hypothenuse}=38 \\ \text{adjacent}=26 \end{gathered}`

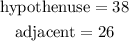
State the relationship between the trigonometry ratio and the sides of the right-angled triangle

`\begin{gathered} \text{Sine}=\frac{opposite}{\text{hypothenuse}} \\ co\sin e=\frac{adjacent}{\text{hypothenuse}} \\ \tan =\frac{opposite}{\text{adjacent}} \end{gathered}`

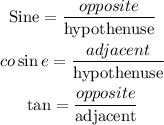
From the given dimension, the appropriate trigonometry to use is cosine

`\cos ?=\frac{\text{adjacent}}{\text{hypothenuse}}=(26)/(38)`
`\begin{gathered} \cos \text{ ?=0.6842} \\ \text{?}=\cos ^(-1)(0.6842) \\ =46.83^0 \end{gathered}`

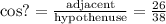
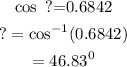
Hence the unknown angle is 46.83°