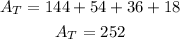ANSWER:
The total surface area of the trapezoidal is 252 m^2
Explanation:
We calculate the surface area of a trapezoid in the following way:
The first thing is to calculate the cross-sectional area:
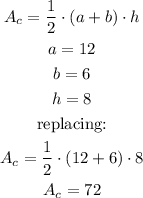
Now we calculate the area of each face, just like this
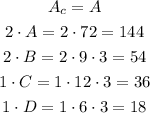
The sums of the area of each area will be the total surface area, we calculate it like this