The system of equations we have to solve is:
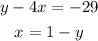
To solve by the substitution method we need to take the second equation of the system and substitute it into the first equation.
In this case, substitute x=1-y in the value of x of the first equation.
Since the first equation is:
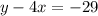
When we substitute the second equation x=1-y, we have:
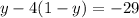
And now that we have an equation that only depends on one variable, we solve for y.
To solve for the value of y, first, we apply the distributive property to multiply -4 by (1-y) and the equation becomes:
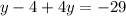
That is because -4(1) is -4 and -4(-y) is equal to 4y.
The next step is to combine the like terms that contain y:
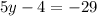
Next, add 4 to both sides of the equation:
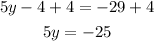
This result is because -4+4 cancels on the left-hand side, and on the right-hand side -29+4 is equal to -25.
The final step is to divide both sides of the equation by 5:
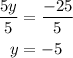
We have one of the variables:
y=-5
To find the value of x, we substitute this value for y into the second equation of the system:
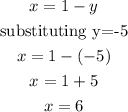
The second variable is x=6
Answer:
x=6 and y=-5