Question

Please help me with this problem I am not able to help my son to understand we keep getting it wrong please help.Kenard takes a square piece of cardboard and cuts 4 in. by 4 in. squares out of each corner. He folds the sides up to make a box without a top.What equation can Kenard use to determine the volume of the box, where x is the side length of the original piece of cardboard? Express the equation in standard form.Enter your answer in the box.V =

Answer 1

Let's draw the figure to better understand the scenario:

Since the cardboard is a "square", all sides must be equal.

The drawing above shows what the sections would look like.

Let's now draw what the box would look like after being cut 4 in. x 4 in. on each corner.

The cardboard formed appears to have the following dimensions:

Length = x - 8

Width = x - 8

Height = 4

In getting the volume of the box, we will be using the following equation:

`\text{ Volume = Length x Width x Height}`

We get,

`\text{ Volume = (x -8)(x - 8)(4) = (4)\lbrack(x - 8)}^2\rbrack`
`\text{ = (4)\lbrack(x)(x) + (x)(-8) + (-8)(x) + (-8)(-8)\rbrack}`
`\text{ = 4(x}^2\text{ - 8x - 8x + 64) = 4(x}^2\text{ - 16x + 64)}`
`\text{ Volume = 4x}^2\text{ - 64x + 256}`

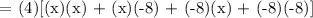
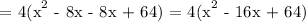
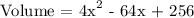
Therefore, the equation to determine the volume of the box is:

Volume = V = 4x² - 64x + 256