Let's draw the figure to better understand the scenario:
Since the cardboard is a "square", all sides must be equal.
The drawing above shows what the sections would look like.
Let's now draw what the box would look like after being cut 4 in. x 4 in. on each corner.
The cardboard formed appears to have the following dimensions:
Length = x - 8
Width = x - 8
Height = 4
In getting the volume of the box, we will be using the following equation:
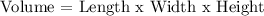
We get,
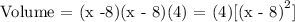
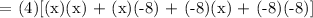
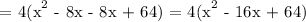
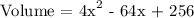
Therefore, the equation to determine the volume of the box is:
Volume = V = 4x² - 64x + 256