Question

Which of the following is the graph of the quadratic function y - x2 +4x-12?Bot-24V2020-2020-20-20AB.C.D.O A. Graph AB. Graph COC. Graph BD. Graph D

Answer 1

option A

Step-by-step explanation:

To detrmine the correct graph, let's find the factors of the function given:

`\begin{gathered} y=x^2\text{ + 4x - 12} \\ \text{The factors of -12 whose sum gives +4 are +6 and - 2} \end{gathered}`
`\begin{gathered} y=x^2\text{ + 6x - 2x - 12} \\ y\text{ = x(x + 6) -2(x + 6)} \\ y\text{ = (x - 2) (x + 6)} \end{gathered}`

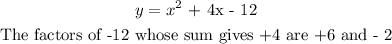
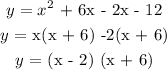
To get the factors equate the function to zero, that is y = 0

`\begin{gathered} 0\text{ = (x -2)(x+6)} \\ x-2\text{ = 0 or x + 6 = 0} \\ x\text{ = 2 or x = -6} \end{gathered}`

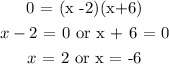
The graph with two x intercepts as 2 and -6 will be the correct quadratic function

Each unit on the graph is 4 units

From the options, option A has x intercepts as 2 and -6