Given
6x -6z =6........Equation (i)
-3x -5y =5 ......Equation (ii)
2y- 6z =4 ........Equation (iii)
Using elimination method
To eliminate X , multiply equation (ii) by 2 and the add
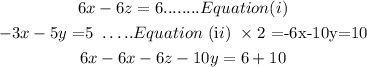
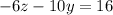
-6z -10y =16 .......Equation (iv)
Rearrange
-10y-6z=16 .......Equation (iv)
2y -6z =4 .......Equation (iii)
To eliminate Z in Equation (iv) and Equation (iii)
Then We subtract
-10y-2y -6z-(-6z) =16 -4
-12y =12
Divide both sides by -12
y= -1
We can substitute for y in equation (iii)
2(-1) -6z=4
-2-6z =4
collect the like terms
-6z= 4+2
-6z=6
Divide both sides by 6
z= -1
Using equation (i)
substitute for z to get x
6x -6(-1) =6
6x +6=6
Collect the like terms
6x = 6-6
6x=0
Divide both sides by 6
x=0
The final answer
X= 0
Y= -1
Z =